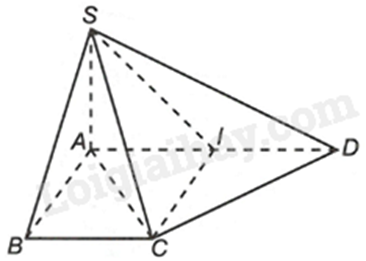
a) Vì \(SA \bot \left( {ABCD} \right),BC \subset \left( {ABCD} \right) \Rightarrow SA \bot BC\).

Vì ABCD là hình thang vuông tại A và B nên \(AB \bot BC\).

Ta có: \(SA \bot BC\), \(AB \bot BC\), SA và AB cắt nhau tại A và nằm trong mặt phẳng (SAB) nên \(BC \bot \left( {SAB} \right)\). Lại có, \(SB \subset \left( {SBC} \right) \Rightarrow BC \bot SB\). Suy ra, tam giác SBC vuông tại B.

b) Gọi I là trung điểm của AD. Do đó, \(AI = ID = \frac{1}{2}AD = a\)

Tứ giác ABCI có: AI//BC (do tứ giác ABCD là hình thang vuông tại A, B), \(AI = BC\left( { = a} \right)\) nên tứ giác ABCI là hình bình hành. Lại có: \(BC = AB\) nên tứ giác ABCI là hình thoi. Mà \(\widehat {BAI} = {90^0}\) nên ABCI là hình vuông. Do đó, \(\widehat {AIC} = {90^0} \Rightarrow \widehat {CID} = {90^0}\)

Tam giác CID có: \(\widehat {CID} = {90^0},CI = ID\left( { = a} \right)\) nên tam giác CID vuông cân tại I.

Suy ra: \(\widehat {DCI} = {45^0}\).

Lại có: CA là phân giác góc ICB (do ABCI là hình vuông) nên \(\widehat {ACI} = \frac{1}{2}\widehat {ICB} = \frac{1}{2}{.90^0} = {45^0}\)

Suy ra: \(\widehat {ACD} = \widehat {ACI} + \widehat {ICD} = {90^0}\) hay \(AC \bot CD\)

Vì \(SA \bot \left( {ABCD} \right),DC \subset \left( {ABCD} \right) \Rightarrow SA \bot DC\)

Ta có: \(AC \bot CD\), \(SA \bot DC\), SA và AC cắt nhau tại A và nằm trong mặt phẳng (SAC) nên \(DC \bot \left( {SAC} \right)\). Mà \(SC \subset \left( {SAC} \right) \Rightarrow CD \bot SC\)