Bài 66 trang 112 SBT Hình học 10 Nâng cao

LG a

Chứng minh rằng với mọi \(M\) thuộc \((E),\) ta luôn có \(b \le OM \le a\).

Lời giải chi tiết:

\(M({x_0} ; {y_0}) \in (E) \)

\(\Rightarrow \dfrac{{x_0^2}}{{{a^2}}} + \dfrac{{y_0^2}}{{{b^2}}} = 1 (a > b > 0) ;\)

\( O{M^2} = x_0^2 + y_0^2\).

Ta có

\(\begin{array}{l} \dfrac{{x_0^2}}{{{a^2}}} + \dfrac{{y_0^2}}{{{a^2}}} \le \dfrac{{x_0^2}}{{{a^2}}} + \dfrac{{y_0^2}}{{{b^2}}} = 1 \\ \Leftrightarrow x_0^2 + y_0^2 \le {a^2} \\ \Leftrightarrow O{M^2} \le {a^2} \Leftrightarrow OM \le a.\\ \dfrac{{x_0^2}}{{{b^2}}} + \dfrac{{y_0^2}}{{{b^2}}} \ge \dfrac{{x_0^2}}{{{a^2}}} + \dfrac{{y_0^2}}{{{b^2}}} = 1 \\\Leftrightarrow x_0^2 + y_0^2 \ge {b^2} \Leftrightarrow O{M^2} \ge {b^2} \\ \Leftrightarrow OM \ge b.\end{array}\)

Vậy \(b \le OM \le a\). Ta có \(a=OM\) khi và chỉ khi \(y_0=0,\) tức là \(M\) trùng với các đỉnh trên trục lớn.

Ta có \(b=OM\) khi và chỉ khi \(x_0=0,\) tức là \(M\) trùng với các đỉnh trên trục bé.

LG b

Gọi \(A\) là giao điểm của đường thẳng có phương trình \(\alpha x + \beta y = 0\) với \((E)\). Tính \(OA\) theo \(a, b, \alpha , \beta \).

Lời giải chi tiết:

Tọa độ điểm \(A\) là nghiệm của hệ

\(\begin{array}{l}\left\{ \begin{array}{l}\alpha x + \beta y = 0\\ \dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\end{array} \right. \\ \Rightarrow x_A^2 = \dfrac{{{a^2}{b^2}{\beta ^2}}}{{{a^2}{\alpha ^2} + {b^2}{\beta ^2}}} , \\ y_A^2 = \dfrac{{{a^2}{b^2}{\alpha ^2}}}{{{a^2}{\alpha ^2} + {b^2}{\beta ^2}}}.\\O{A^2} = x_A^2 + y_A^2\\ = \dfrac{{{a^2}{b^2}{\beta ^2}}}{{{a^2}{\alpha ^2} + {b^2}{\beta ^2}}} + \dfrac{{{a^2}{b^2}{\alpha ^2}}}{{{a^2}{\alpha ^2} + {b^2}{\beta ^2}}}\\ = \dfrac{{{a^2}{b^2}({\alpha ^2} + {\beta ^2})}}{{{a^2}{\alpha ^2} + {b^2}{\beta ^2}}}.\\ \Rightarrow OA = \dfrac{{ab.\sqrt {{\alpha ^2} + {\beta ^2}} }}{{\sqrt {{a^2}{\alpha ^2} + {b^2}{\beta ^2}} }}.\end{array}\)

LG c

Gọi \(B\) là điểm trên \((E)\) sao cho \(OA \bot OB\). Chứng minh rằng tổng \( \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}}\) có giá trị không đổi.

Lời giải chi tiết:

Do \(OA\) vuông góc với \(OB\) nên phương trình đường thẳng \(OB\) là: \(\beta x - \alpha y = 0\). \(B\) là giao điểm của \((E)\) với đường thẳng \(\beta x + ( - \alpha )y = 0\) nên áp dụng câu b), ta có

\(O{B^2} = \dfrac{{{a^2}{b^2}\left[ {{\beta ^2} + {{( - \alpha )}^2}} \right]}}{{{a^2}{\beta ^2} + {b^2}{{( - \alpha )}^2}}}\)

\(= \dfrac{{{a^2}{b^2}({\alpha ^2} + {\beta ^2})}}{{{a^2}{\beta ^2} + {b^2}{\alpha ^2}}}.\)

Do đó :

\( \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}}\)

\(= \dfrac{{{a^2}{\alpha ^2} + {b^2}{\beta ^2} + {a^2}{\beta ^2} + {b^2}{\alpha ^2}}}{{{a^2}{b^2}({\alpha ^2} + {\beta ^2})}} \)

\(= \dfrac{{{a^2} + {b^2}}}{{{a^2}{b^2}}}\) không đổi.

LG d

Chứng minh rằng đường thẳng \(AB\) luôn tiếp xúc với một đường tròn cố định.

Lời giải chi tiết:

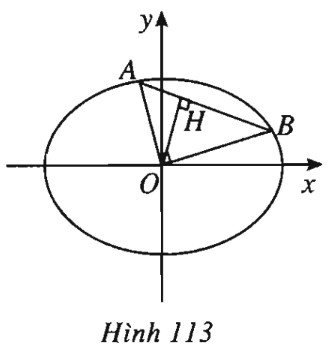
Kẻ \(OH \bot AB\). Trong tam giác vuông \(AOB,\) ta có

\(\begin{array}{l} \dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} = \dfrac{{{a^2} + {b^2}}}{{{a^2}{b^2}}}\\ \Rightarrow OH = \dfrac{{ab}}{{\sqrt {{a^2} + {b^2}} }}.\end{array}\)

Vậy đường thẳng \(AB\) luôn tiếp xúc với đường tròn cố định tâm \(O,\) bán kính \(R = \dfrac{{ab}}{{\sqrt {{a^2} + {b^2}} }}\).

xemloigiai.com