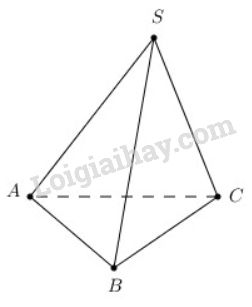
Bài 5 trang 98 SGK Hình học 11Cho hình chóp tam giác S.ABC có SA = SB = SC... Đề bài Cho hình chóp tam giác \(S.ABC\) có \(SA = SB = SC\) và có \(\widehat{ASB}= \widehat{BSC}=\widehat{CSA}.\) Chứng minh rằng \(SA ⊥ BC, SB ⊥ AC, SC ⊥ AB\). Phương pháp giải - Xem chi tiết Chứng minh \(\overrightarrow {SA} .\overrightarrow {BC} = 0;\,\,\overrightarrow {SB} .\overrightarrow {AC} = 0;\,\,\overrightarrow {SC} .\overrightarrow {AB} = 0\) Sử dụng công thức tính tích vô hướng: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \widehat {\left( {\overrightarrow a ;\overrightarrow b } \right)}\) Lời giải chi tiết
\(\overrightarrow{SA}.\overrightarrow{BC}=\overrightarrow{SA}.(\overrightarrow{SC}-\overrightarrow{SB})\) \(=\overrightarrow{SA}.\overrightarrow{SC}-\overrightarrow{SA}.\overrightarrow{SB}\) \(= SA.SC.\cos\widehat{ASC} - SA.SB.\cos\widehat{ASB} = 0\) Vậy \(SA ⊥ BC\). \(\overrightarrow{SB}.\overrightarrow{AC}=\overrightarrow{SB}.(\overrightarrow{SC}-\overrightarrow{SA})\) \(=\overrightarrow{SB}.\overrightarrow{SC}-\overrightarrow{SB}.\overrightarrow{SA}\) \(= SB.SC.\cos\widehat{BSC} - SB.SA.\cos\widehat{ASB} = 0\) Vậy \(SB ⊥ AC\). \(\overrightarrow{SC}.\overrightarrow{AB}=\overrightarrow{SC}.(\overrightarrow{SB}-\overrightarrow{SA})\) \(=\overrightarrow{SC}.\overrightarrow{SB}-\overrightarrow{SC}.\overrightarrow{SA}\) \(= SC.SB.\cos\widehat{BSC} - SC.SA.\cos\widehat{ASC} = 0\) Vậy \(SC ⊥ AB\). xemloigiai.com
2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!
|
