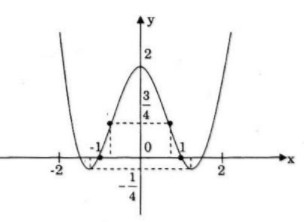
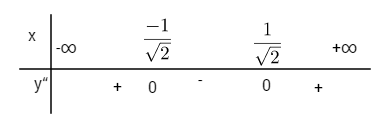Bài 44 trang 44 SGK giải tích 12 nâng cao

LG a

\(y = {x^4} - 3{x^2} + 2\)

Lời giải chi tiết:

TXĐ: \(D =\mathbb R\)

\(\eqalign{
& \mathop {\lim }\limits_{x \to \pm \infty } y = + \infty \cr 
& y' = 4{x^3} - 6x\cr&y' = 0 \Leftrightarrow \left[ \matrix{
x = 0; \hfill \cr 
x = \pm \sqrt {{3 \over 2}} \hfill \cr} \right. \cr} \)

\(y\left( 0 \right) = 2\) và \(y\left( { \pm \sqrt {{3 \over 2}} } \right) = - {1 \over 4}\)

Bảng biến thiên:

\(y'' = 12{x^3} - 6\)

\(y'' = 0 \Leftrightarrow x = \pm \sqrt {{1 \over 2}} \)

\(y = \left( { \pm \sqrt {{1 \over 2}} } \right) = {3 \over 4}\)
Xét dấu \(y”\)
 
Đồ thị có hai điểm uốn \({I_1}\left( { - \sqrt {{1 \over 2}} ;{3 \over 4}} \right)\) và \({I_2}\left( {\sqrt {{1 \over 2}} ;{3 \over 4}} \right)\)
Điểm đặc biệt: \(x = \pm 1 \Leftrightarrow y = 0,x = \pm \sqrt 2 \Leftrightarrow y = 0.\)
Đồ thị: Đồ thị nhận trục tung làm trục đối xứng.

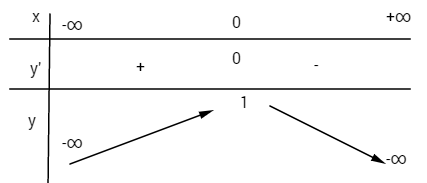
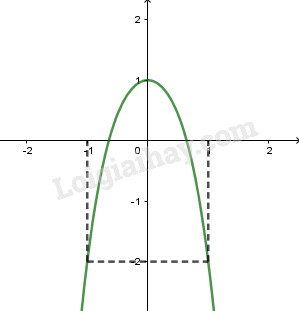
LG b

\(y = - {x^4} - 2{x^2} + 1\)

Lời giải chi tiết:

TXĐ: \(D =\mathbb R\)

\(\eqalign{
& \mathop {\lim }\limits_{x \to \pm \infty } y = - \infty \cr 
& y' = - 4{x^3} - 4x = - 4x\left( {{x^2} + 1} \right) \cr 
& y' = 0 \Leftrightarrow x = 0;y\left( 0 \right) = 1 \cr} \)

Bảng biến thiên:

\(y'' = - 12{x^2} - 4 = - 4\left( {3{x^2} + 1} \right) < 0\) với mọi \(x\)
Đồ thị không có điểm uốn.

Điểm đặc biệt \(x = \pm 1 \Rightarrow y = - 2\)
Đồ thị:

Đồ thị nhận trục tung làm trục đối xứng.

xemloigiai.com