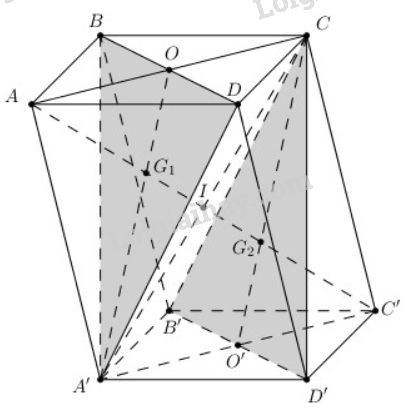
Bài 3 trang 71 SGK Hình học 11

Đề bài

Cho hình hộp \(ABCD.A'B'C'D'\).

a) Chứng minh rằng hai mặt phẳng \((BDA')\) và \((B'D'C)\) song song với nhau.

b) Chứng minh rằng đường chéo \(AC'\) đi qua trọng tâm \({G_{1},{G_{2}}}\) của hai tam giác \(BDA'\) và \(B'D'C\).

c) Chứng minh \({G_{1},{G_{2}}^{}}^{}\) chia đoạn \(AC'\) thành ba phần bằng nhau.

d) Gọi \(O\) và \(I\) lần lượt là tâm của các hình bình hành \(ABCD\) và \(AA'C'C\). Xác định thiết diện của mặt phẳng \((A'IO)\) với hình hộp đã cho. 

Lời giải chi tiết

a) Ta có: \(BDD'B'\) là hình bình hành ( vì \(BB'//DD'; BB'=DD' \)).

\(\Rightarrow BD//B'D'\)

Mà \(BD \not\subset \left( {CB'D'} \right)\) nên \(BD // \left( {CB'D'} \right)\). 

Tương tự, ta cũng suy ra \(A'B // \left( {CB'D'} \right)\). 

Mặt khác: \(BD, A'B\) cắt nhau trong mp \((BDA')\)

\(\Rightarrow (BDA')//(CB'D')\).

b)

Cách 1:

Gọi \(O,O'\) lần lượt là tâm của hình bình hành \(ABCD,A'B'C'D'\), \({G_{1}}^{}\), \({G_{2}}^{}\) là giao điểm của \(AC'\) với \(A'O\) và \(CO'\)

\(\Delta {G_1}OA\) đồng dạng \(\Delta {G_1}A'C'\) (g.g)

\( \Rightarrow \dfrac {{G_1}O} {{G_1}A'} = \dfrac{OA} {A'C'} = \dfrac 1 2 \)

\(\Rightarrow \dfrac {A'{G_1}} {A'O} =\dfrac 2 3.\)

Lại có \({G_1} \in A'O\) là đường trung tuyến của \(\Delta BDA'\) \(\Rightarrow G_1\) là trọng tâm \(\Delta A'BD.\)

Chứng minh tương tự ta có: \(G_2\) là trọng tâm \(\Delta B'D'C.\) 

Vậy \(AC'\) đi qua \(G_1,G_2\) lần lượt là trọng tâm của hai tam giác \(BDA'\) và \(B'D'C\).

Cách 2:

Gọi \(I = A'C \cap AC'\)

Ta có: \(ABCD\) và \(ACC'A'\) là các hình bình hành, \(O\) và \(I\) lần lượt là giao điểm 2 đường chéo.

Suy ra \(O\) và \(I\) lần lượt là trung điểm của \(AC\) và \(A'C\).

Xét \(\Delta A'AC\) ta có:

\(A'O, AI\) là trung tuyến, cắt nhau tại \({G_1}\)

\( \Rightarrow{G_1}\) là trọng tâm \(\Delta A'AC\)

\( \Rightarrow{A'G_1} = \frac {2}{3} A'O\).

Mà \(A'O\) cũng là trung tuyến của \(\Delta A'BD\)

\( \Rightarrow{G_1}\) là trọng tâm \(\Delta A'BD\).

Chứng minh tương tự, ta cũng suy ra \({G_2}\) là trọng tâm \(\Delta CB'D'\).

c)

Ta có:

\( \dfrac{A{G_{1}}^{}}{{G_{1}C'}}\) = \( \dfrac{AO}{A'C'} = \dfrac{1}{2}\) (vì \(\Delta G_1OA\) đồng dạng \(\Delta G_1 A'C'\)) \( \Rightarrow A{G_1} = \frac{1}{3}AC'\).

Từ đó suy ra: \( AG_{1} = G_{1}G_{2}= G_{2}C'\)

d) Vì \((A'IO) ≡ (AA'C'C)\) suy ra thiết diện của hình hộp khi cắt bởi mặt phẳng \((A'IO)\) là thiết diện khi cắt bởi mp\((AA'C'C)\), chính là hình bình hành \(AA'C'C\).

xemloigiai.com