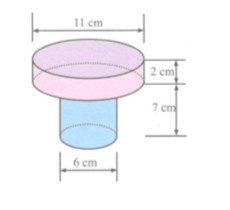
Bài 22 trang 143 Tài liệu dạy – học Toán 9 tập 2

Đề bài

Hãy tính thể tích, diện tích bề mặt một chi tiết máy theo kích thước đã cho trong hình sau:

Lời giải chi tiết

Chi tiết máy được tạp nên bởi 2 hình trụ.

Hình trụ thứ nhất có bán kính đáy ${R_1} = 5,5cm$, chiều cao ${h_1} = 2cm$

$\Rightarrow$ Diện tích toàn phần của hình trụ thứ nhất là

${S_{tp1}} = 2\pi {R_1}{h_1} + 2\pi R_1^2$$\,= 2\pi .5,5.2 + 2\pi {.2^2} = 30\pi \,\,\left( {c{m^2}} \right)$

Thể tích của hình trụ thứ nhất là ${V_1} = \pi R_1^2{h_1} = \pi .5,{5^2}.2 = \dfrac{{121\pi }}{2}\,\,\left( {c{m^3}} \right)$.

Hình trụ thứ nhất có bán kính đáy ${R_2} = 3cm$, chiều cao ${h_1} = 7cm$

$\Rightarrow$ Diện tích toàn phần của hình trụ thứ nhất là

${S_{tp2}} = 2\pi {R_2}{h_2} + 2\pi R_2^2$$\, = 2\pi .3.7 + 2\pi {.3^2} = 60\pi \,\,\left( {c{m^2}} \right)$

Thể tích của hình trụ thứ nhất là ${V_2} = \pi R_2^2{h_2} = \pi {.3^2}.7 = 63\pi \,\,\left( {c{m^3}} \right)$.

Do phần diện tích tiếp xúc giữa 2 hình trụ được tính 2 lần nên diện tích bề mặt của chi tiết máy là

$S = {S_{tp1}} + {S_{tp2}} - {S_{tx}}$$\,= 30\pi + 60\pi - \pi {.3^2} = 81\pi \,\,\left( {c{m^2}} \right)$.

Thể tích của chi tiết máy là $V = {V_1} + {V_2} = \dfrac{{121}}{2}\pi + 63\pi = \dfrac{{247}}{2}\pi \,\,\left( {c{m^3}} \right)$. 

 xemloigiai.com