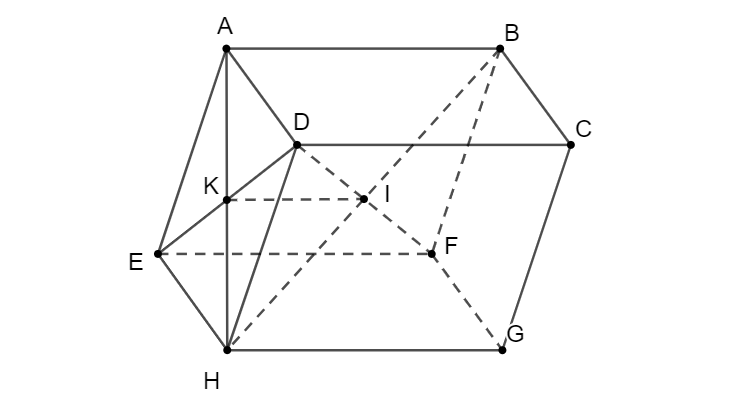
Bài 10 trang 92 SGK Hình học 11

Đề bài

Cho hình hộp \(ABCD.EFGH\). Gọi \(K\) là giao điểm của \(AH\) và \(DE\), \(I\) là giao điểm của \(BH\) và \(DF\). Chứng minh ba véctơ \(\overrightarrow{AC}\), \(\overrightarrow{KI}\), \(\overrightarrow{FG}\) đồng phẳng.

Quảng cáo

Lời giải chi tiết

\(I=BH\cap DF\) là giao điểm của hai đường chéo hình bình hành \(BDHF\) do đó \(I\) là trung điểm của \(BH\).

\(K\) là giao điểm của hai đường chéo hình bình hành \(ADHE\) do đó \(K\) là trung điểm của \(AH\).

\(\Rightarrow KI\) là đường trung bình của tam giác \(ABH\).

\(\Rightarrow KI//AB \Rightarrow KI//(ABCD)\) (1)

Ta có: \(BCGF\) là hình bình hành

\(\Rightarrow FG//BC \Rightarrow FG//(ABCD)\) (2)

Từ (1) và (2) suy ra: các véctơ \(\overrightarrow{KI}\), \(\overrightarrow{FG}\) song song với mặt phẳng \((ABCD)\) chứa véctơ \(\overrightarrow{AC}\)

Vậy \(\overrightarrow{AC}\), \(\overrightarrow{KI}\), \(\overrightarrow{FG}\) đồng phẳng.

 xemloigiai.com