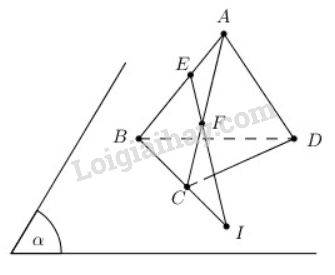
Bài 1 trang 53 SGK Hình học 11

Đề bài

Cho điểm \(A\) không nằm trong mặt phẳng \((α)\) chứa tam giác \(BCD\). Lấy \(E,F\) là các điểm lần lượt nằm trên các cạnh \(AB, AC\).

a) Chứng minh đường thẳng \(EF\) nằm trong mặt phẳng \((ABC)\).

b) Khi \(EF\) và \(BC\) cắt nhau tại \(I\), chứng minh \(I\) là điểm chung của hai mặt phẳng \((BCD)\) và \((DEF)\).

Quảng cáo

Lời giải chi tiết

a) Ta có: 

\(\left\{ \begin{array}{l}
E \in AB,\,\,AB \subset \left( {ABC} \right) \Rightarrow E \in \left( {ABC} \right)\\
F \in AC,\,\,AC \subset \left( {ABC} \right) \Rightarrow F \in \left( {ABC} \right)
\end{array} \right.\)

Theo tính chất 3, đường thẳng \(EF\) có hai điểm \(E, F\) cùng thuộc mặt phẳng \((ABC)\) nên \( EF \subset \left( {ABC} \right)\)

b) Ta có:

\(\left\{ \begin{array}{l}I \in EF,\,\,EF \subset \left( {DEF} \right) \Rightarrow I \in \left( {DEF} \right)\\I \in BC,\,\,BC \subset \left( {BCD} \right) \Rightarrow I \in \left( {BCD} \right)\end{array} \right. \)\(\,\Rightarrow I\) là điểm chung của hai mặt phẳng \((BCD)\) và \((DEF)\).

xemloigiai.com