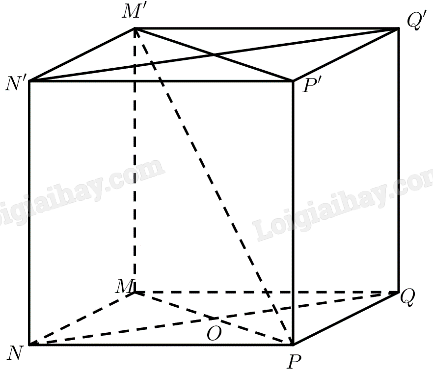
Bài 1 trang 116 SGK Toán 11 tập 2 - Cánh DiềuCho hình lập phương \(MNPQ.M'N'P'Q'\) có cạnh bằng \(a\). Tổng hợp đề thi giữa kì 2 lớp 11 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh Đề bài Cho hình lập phương \(MNPQ.M'N'P'Q'\) có cạnh bằng \(a\). a) Góc giữa hai đường thẳng \(MN\) và \(M'P\) bằng: A. \({30^ \circ }\). B. \({45^ \circ }\). C. \({60^ \circ }\). D. \({90^ \circ }\). b) Gọi \(\alpha \) là số đo góc giữa đường thẳng \(M'P\) và mặt phẳng \(\left( {MNPQ} \right)\). Giá trị \(\tan \alpha \) bằng: A. 1. B. 2. C. \(\sqrt 2 \). D. \(\frac{1}{{\sqrt 2 }}\). c) Số đo của góc nhị diện \(\left[ {N,MM',P} \right]\) bằng: A. \({30^ \circ }\). B. \({45^ \circ }\). C. \({60^ \circ }\). D. \({90^ \circ }\). d) Khoảng cách từ điểm \(M\) đến mặt phẳng \(\left( {NQQ'N'} \right)\) bằng: A. \(a\). B. \(\frac{a}{{\sqrt 2 }}\). C. \(a\sqrt 2 \). D. \(\frac{a}{2}\). Phương pháp giải - Xem chi tiết a) Cách xác định góc giữa hai đường thẳng \(a\) và \(b\): Bước 1: Lấy một điểm \(O\) bất kì. Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\). Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\). b) Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng. c) Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\) Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\). Bước 2: Tìm mặt phẳng \(\left( R \right) \bot c\). Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\). Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\). d) Cách tính khoảng cách từ một điểm đến một mặt phẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên mặt phẳng. Quảng cáo  Lời giải chi tiết
a) \(MM' = PP',MM'\parallel PP'\) \( \Rightarrow MPP'M'\) là hình bình hành \( \Rightarrow MP\parallel M'P' \Rightarrow \left( {MN,M'P'} \right) = \left( {MN,MP} \right) = \widehat {NMP}\) \(MNPQ\) là hình vuông \( \Rightarrow \widehat {NMP} = {45^ \circ }\) Vậy . Chọn B. b) \(MM' \bot \left( {MNPQ} \right) \Rightarrow \left( {M'P,\left( {MNPQ} \right)} \right) = \left( {M'P,MP} \right) = \widehat {MPM'}\) \(MNPQ\) là hình vuông \( \Rightarrow MP = \sqrt {M{N^2} + N{P^2}} = a\sqrt 2 \) \(\tan \widehat {MPM'} = \frac{{MM'}}{{MP}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }}\) Chọn D. c) \(MM' \bot \left( {MNPQ} \right) \Rightarrow MM' \bot MN,MM' \bot MP\) Vậy \(\widehat {NMP} = {45^ \circ }\) là góc nhị diện \(\left[ {N,MM',P} \right]\). Chọn B. d) Gọi \(O = MP \cap NQ\) \(MNPQ\) là hình vuông \( \Rightarrow MO \bot NQ\) \(NN' \bot \left( {MNPQ} \right) \Rightarrow NN' \bot MO\) \( \Rightarrow d\left( {M,\left( {NQQ'N'} \right)} \right) = MO = \frac{1}{2}MP = \frac{a}{{\sqrt 2 }}\). Chọn B.
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
|
